Propriété de Markov simple - Math'φsics

Propriété de Markov simple

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent

Propriété de Markov simple/faible - cas général :
\(n\geqslant0\)

\(F,G\) sont deux Fonction mesurables positives sur \(\Omega^\circ=E^{\Bbb N}\)

\(F\) est \({\mathcal F}_n\)-mesurable

$$\Huge\iff$$

$${\Bbb E}_x[F\times G\circ\theta_n]={\Bbb E}_x[F{\Bbb E}_{X_n}[G]]$$

de manière équivalente, $${\Bbb E}_x[G\circ\theta_n|{\mathcal F}_n]={\Bbb E}_{X_n}[G]$$
Démontrer \((**)\) :

On suppose d'abord que \(F\) est une indicatrice d'un cylindre \(\to\) on connaît alors \(\Bbb 1_A\circ\theta_n\).

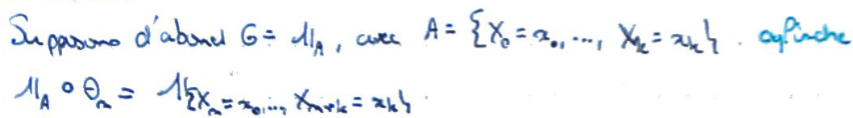
On calcule l'espérance conditionnelle de \(F\) sachant \(X_0,\dots,X_n\).

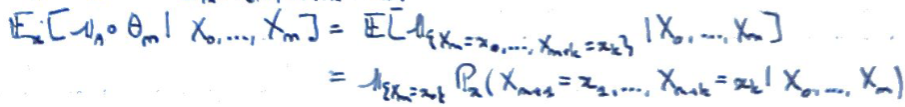
Cette probabilité peut facilement être calculée à l'aide d'une proposition précédente.

Généralisation par Lemme de classe monotone, linéarité et densité.
Rétroliens :
- Propriété de Markov forte